Python basics 2: Numpy

This tutorial introduces numpy (pronounced num-pye, rhymes with eye), a Python library for performing numerical computations in Python. We will learn how to create and manipulate numpy arrays, which are useful matrix-like structures for holding large amounts of data.

Follow the instructions below to download the tutorial and open it in the Sandbox.

Download the tutorial notebook

Download the Python basics 2 tutorial notebook

To view this notebook on the Sandbox, you will need to first download it to your computer, then upload it to the Sandbox. Ensure you have followed the set-up prerequisities listed in Python basics 1: Jupyter, and then follow these instructions:

1. Download the notebook by clicking the link above.

2. On the Sandbox, open the Training folder.

3. Click the Upload Files button as shown below.

4. Select the downloaded notebook using the file browser. Click OK.

5. The solution notebook will appear in the Training folder. Double-click to open it.

You can now use the tutorial notebook as an interactive version of this webpage.

Note

The tutorial notebook should look like the text and code below. However, the tutorial notebook outputs are blank (i.e. no results showing after code cells). Follow the instructions in the notebook to run the cells in the tutorial notebook. Refer to this page to check your outputs look similar.

Introduction to numpy

In order to be able to use numpy we need to import the numpy library using the special word import. To avoid typing numpy every time we want to use one of its functions, we can provide an alias using the special word as. We will nickname numpy as np:

import numpy as np

Note: If we do not import numpy, we cannot use any of the numpy functions. If you forget to import packages, you may get an error that says name is not defined.

Now, we have access to all the functions available in numpy by typing np.name_of_function. For example, the equivalent of 1 + 1 in Python can be done in numpy:

np.add(1,1)

2

By default the result of a function or operation is shown underneath the cell containing the code. If we want to reuse this result for a later operation we can assign it to a variable. For instance, let us call the variable a:

a = np.add(2,3)

We have just declared a variable a that holds the result of the function. We can now use of display this variable, at any point of this notebook. For example we can show its contents by typing the variable name in a new cell:

a

5

One of numpy’s core concepts is the array. They can hold multi-dimensional data. To declare a numpy array explicity we do:

np.array([1,2,3,4,5,6,7,8,9])

array([1, 2, 3, 4, 5, 6, 7, 8, 9])

Note: The array defined above has only 1 dimension.

Most of the functions and operations defined in numpy can be applied to arrays. For example, with the previous add operation:

arr1 = np.array([1,2,3,4])
arr2 = np.array([3,4,5,6])

np.add(arr1, arr2)

array([ 4,  6,  8, 10])

We can also add arrays using the following convenient notation:

arr1 + arr2

array([ 4,  6,  8, 10])

Arrays can be sliced and diced. We can get subsets of the arrays using the indexing notation which is [ start : end : stride ]. Let’s see what this means:

arr = np.array([0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15])

print(arr[5])
print(arr[5:])
print(arr[:5])
print(arr[::2])

5
[ 5  6  7  8  9 10 11 12 13 14 15]
[0 1 2 3 4]
[ 0  2  4  6  8 10 12 14]

Experiment playing with the indexes to understand the meaning of start, end and stride. What happens if you don’t specify a start? What value does numpy use instead?

Note: Numpy indexes start on 0, the same convention used in Python lists.

Indexes can also be negative, meaning that you start counting by the end. For example, to select the last 2 elements in an array we can do:

arr = np.array([0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15])

arr[-2:]

array([14, 15])

Numpy arrays can have multiple dimensions. Dimensions are indicated using nested square brackets [ ]. The convention in numpy is that the outer [ ] represent the first dimension and the innermost [ ] contains the last dimension.

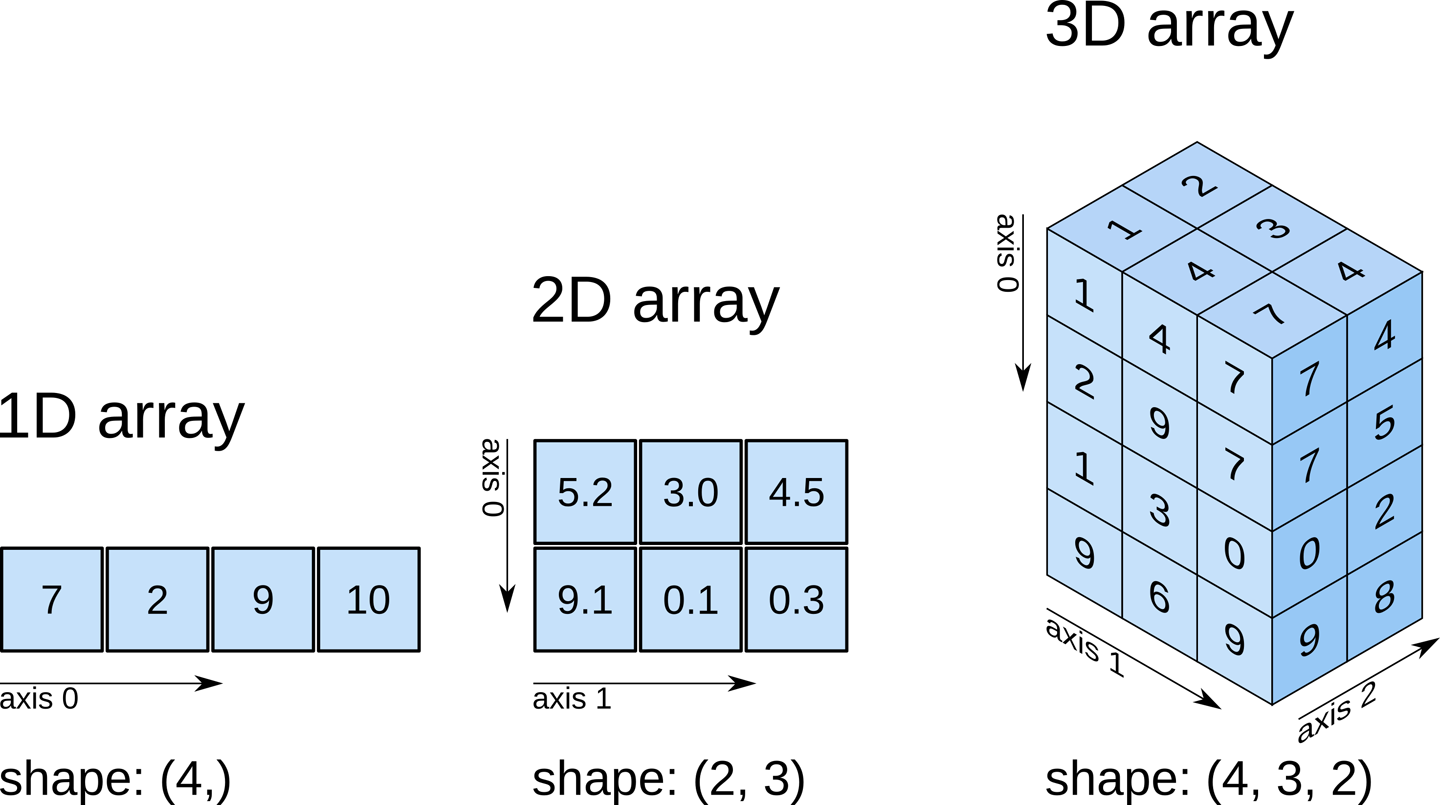
The following cell declares a 2-dimensional array with shape (1, 9).

Tip: Notice the nested (double) square brackets [[ ]]. As there are two brackets, this indicates the array is 2-dimensional.

np.array([[1,2,3,4,5,6,7,8,9]])

array([[1, 2, 3, 4, 5, 6, 7, 8, 9]])

To visualise the shape (dimensions) of a numpy array we can add the suffix .shape to an array expression or variable containing a numpy array.

arr1 = np.array([1,2,3,4,5,6,7,8,9])
arr2 = np.array([[1,2,3,4,5,6,7,8,9]])
arr3 = np.array([[1],[2],[3],[4],[5],[6],[7],[8],[9]])

arr1.shape, arr2.shape, arr3.shape, np.array([1,2,3]).shape

((9,), (1, 9), (9, 1), (3,))

Numpy arrays can contain numerical values of different types. These types can be divided in these groups:

• Integers

  • Unsigned

    • 8 bits: uint8

    • 16 bits: uint16

    • 32 bits: uint32

    • 64 bits: uint64

  • Signed

    • 8 bits: int8

    • 16 bits: int16

    • 32 bits: int32

    • 64 bits: int64

• Floats

  • 32 bits: float32

  • 64 bits: float64

We can look up the type of an array by using the .dtype suffix.

arr = np.ones((10,10,10))

arr.dtype

dtype('float64')

Numpy arrays normally store numeric values but they can also contain boolean values, 'bool'. Boolean is a data type that can have two possible values: True, or False. For example:

arr = np.array([True, False, True])

arr, arr.shape, arr.dtype

(array([ True, False,  True]), (3,), dtype('bool'))

We can operate with boolean arrays using the numpy functions for performing logical operations such as and and or.

arr1 = np.array([True, True, False, False])
arr2 = np.array([True, False, True, False])

print(np.logical_and(arr1, arr2))
print(np.logical_or(arr1, arr2))

[ True False False False]
[ True  True  True False]

These operations are conveniently offered by numpy with the symbols * (and), and + (or).

Note: Here the * and + symbols are not performing multiplication and addition as with numerical arrays. Numpy detects the type of the arrays involved in the operation and changes the behaviour of these operators.

print(arr1 * arr2)
print(arr1 + arr2)

[ True False False False]
[ True  True  True False]

Boolean arrays are often the result of comparing a numerical arrays with certain values. This is sometimes useful to detect values that are equal, below or above a number in a numpy array. For example, if we want to know which values in an array are equal to 1, and the values that are greater than 2 we can do:

arr = np.array([1, 3, 5, 1, 6, 3, 1, 5, 7, 1])

print(arr == 1)
print(arr > 2)

[ True False False  True False False  True False False  True]
[False  True  True False  True  True False  True  True False]

You can use a boolean array to mask out False values from a numeric array. The returned array only contains the numeric values which are at the same index as True values in the mask array.

arr = np.array([1,2,3,4,5,6,7,8,9])
mask = np.array([True,False,True,False,True,False,True,False,True])

arr[mask]

array([1, 3, 5, 7, 9])

Exercises

2.1 Use the numpy add function to add the values 34 and 29 in the cell below.

# Use numpy add function to add 34 and 29

2.2 Declare a new array with contents [5,4,3,2,1] and slice it to select the last 3 items.

# Substitute the ? symbols by the correct expressions and values

# Declare the array

arr = ?

# Slice array for the last 3 items only

arr[?:?]

2.3 Select all the elements in the array below excluding the last one, [15].

arr = np.array([0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15])

# Substitute the ? symbols by the correct expressions and values

arr[?]

2.4 Use arr as defined in 2.3. Exclude the last element from the list, but now only select every 3rd element. Remember the third index indicates stride, if used.

Hint: The result should be [0,3,6,9,12].

# Substitute the ? symbols by the correct expressions and values

arr[?:?:?]

2.5 You’ll need to combine array comparisons and logical operators to solve this one. Find out the values in the following array that are greater than 3 AND less than 7. The output should be a boolean array.

Hint: If you are stuck, reread the section on boolean arrays.

arr = np.array([1, 3, 5, 1, 6, 3, 1, 5, 7, 1])

# Use array comparisons (<, >, etc.) and logical operators (*, +) to find where
# the values are greater than 3 and less than 7.

boolean_array = ?

2.6 Use your boolean array from 2.5 to mask the False values from arr.

Hint: The result should be [5, 6, 5].

# Use your resulting boolean_array array from 2.5
# to mask arr as defined in 2.5

Conclusion

Numpy is a fundamental numerical computing library in Python programming and it is useful to understand how it works. Next, we explore plotting geospatial data using matplotlib.